Théorie des Graphes

Vassilis GIAKOUMAKIS vassilis.giakoumakis@u-picardie.fr Sébastien CHOPLIN sebastien.choplin@u-picardie.fr

Notions de base

1. Introduction
2. Définitions
   1. Graphe orienté
   2. Graphe non orienté
   3. Boucle
   4. Multigraphe
   5. ??
   6. Symétrie
3. Notations

1. Introduction

   La théorie des graphes est une des branches les plus florissantes de l'algèbre moderne. Le graphe est un modèle mathématique très puissant qui est utilisé dans presque toutes les sciences.

   Le début de la théorie des graphes est considéré l'année 1736 lorsqu'Euler a résolu un problème qui passionnait les habitants de la ville de Koenisgsberg (ajourd'hui appelée Kaliningrad):
   

   Un piéton peut-il, en se promenant, traverser une fois et une seule les 7 ponts de la rivière Pregel qui traverse la ville ?

   

2. Définitions
   1. Graphe orienté

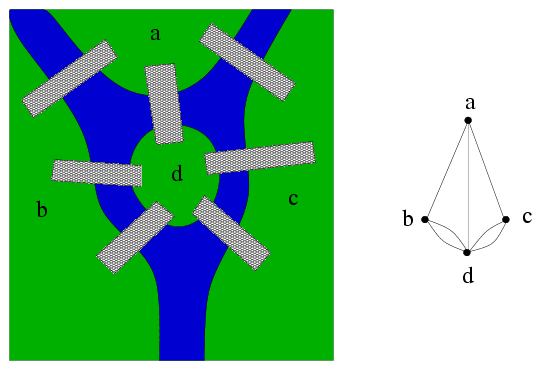
      Un graphe orienté G=(S,A) est une couple formé d'un ensemble de sommets S et un ensemble de couples de sommets A, appelés arcs.

      

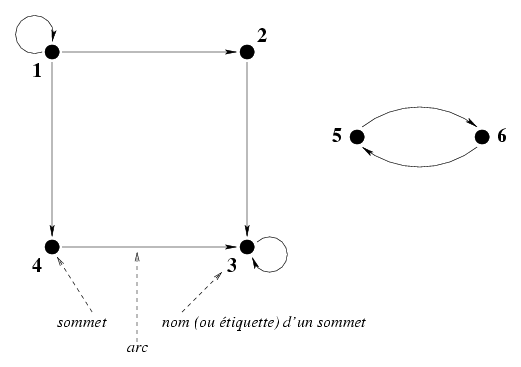
      Dans cet exemple l'ensemble de sommets S est {1,2,3,4,5,6}, l'ensemble des arcs A est {(1,1),(1,2),(2,3),(3,3),(4,3),(1,4)}.

      Remarque: on utilise les "parenthèses" ( ) pour décrire un couple (dans un couple les éléments sont ordonnés).

      Etant donné un arc u=(x,y), le sommet x est l'extrémité initiale de u et y est l'extrémité terminale. On dira aussi que u est incident à x vers l'extérieur et incident à y vers l'intérieur. Enfin, on dira que x est un prédécesseur de y et y un successeur de x.

   2. Graphe non orienté

      Un graphe non orienté G=(S,A) est une couple formé d'un ensemble de sommets S et un ensemble de paires de sommets A, appelés arêtes.

      

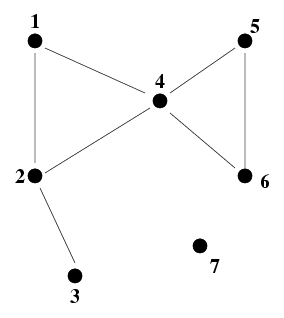
      Dans cet exemple l'ensemble de sommets S est {1,2,3,4,5,6,7}, l'ensemble des arêtes A est {[1,2],[2,3],[1,4],[4,5],[4,6],[5,6]}.

      Remarque: on utilise les "crochets" [ ] pour décrire une paire (dans une paire les éléments ne sont pas ordonnés).

      Etant donné une ar u=[x,y], x et y sont ses deux extrémités. On dira que x et y sont adjacents ou voisins.

   3. Boucle

      Une boucle est une arête reliant un sommet avec lui-même. Par exemple: (x,x).

   4. Multigraphe

      Lorsqu'entre deux sommets x et y de G il existe plus d'un arc de x vers y (ou plus d'une arêtes ou une boucle), on dira que G est un multigraphe.

   5. ??

      Soit G=(S,A) un graphe orienté. Le graphe non orienté correspondant à G sera la graphe G'=(S,A') avec A'={ [x,y] | (x,y) ou (y,x) ∈ A et x≠y }

   6. Symétrie

      Un graphe est dit symétrique si la propriété suivante est vraie:

      (x,y) ∈ A ⇒ (y,x) ∈ A
      i.e.: si l'arête (x,y) est dans A alors l'arête (y,x) est aussi dans A.

      Dans la communauté mathématique et informatique, il y a des écoles qui n'acceptent pas la distinction entre graphe orienté et non orienté: un graphe non orienté sera tout simplement un graphe symétrique sans boucles. En ce qui nous concerne, nous maintiendrons cette disctinction.

      1. Antisymétrie

         Soit G=(S,A) un graphe orienté. G est dit antisymétrique si quelques soient x et y avec x≠y, la propriété suivante est vraie:

         (x,y) &isin A &rArr (y,x) ∉ A

      2. Asymétrie

         Soit G=(S,A) un graphe orienté. G est dit asymétrique si quelques soient x et y, la propriété suivante est vraie:

         (x,y) &isin A &rArr (y,x) ∉ A
         (G asymétrique ⇒ G n'a pas de boucles.)

      3. Complet

         Soit G=(S,A) un graphe orienté. G est dit complet si la propriété suivante est vraie:

         (x,y) ¬in A &rArr (y,x) ∈ A
         CONFLIT AVEC LA DEFINITION DE GRAPHE COMPLET ???

3. Notations

   On décira dans la suite par n le nombre de sommets de G et par m le nombre de ses arêtes (ou arcs s'il s'agit d'un graphe orienté).