Le but est de donner la matrice de transformation 3D permettant de déterminer la position d'un point de la terre en coordonnées héliocentriques en fonction du jour de l'année et de l'heure du jour, connaissant sa position le premier jour de l'année à 00h00.

En même temps que son mouvement de révolution autour du Soleil, la Terre est animée d'un mouvement de rotation autour de son axe Nord-Sud. Cette rotation s'effectue en 24H.

L'axe de rotation de la Terre n'est pas perpendiculaire au plan de l'écliptique : l'équateur terrestre fait avec l'écliptique un angle d'environ 24° (Cet angle d'inclinaison est responsable du phénomène des saisons sur Terre).
Question 2: en admettant que la Terre ne tourne pas autour du soleil, donner la matrice de transformation 3D permettant de donner la position d'un point de la terre au bout de t secondes (0<=t<=3600*24) en fonction de sa position à t=0.
Question 3: donner la matrice de transformation 3D permettant de donner la position d'un point de la terre.
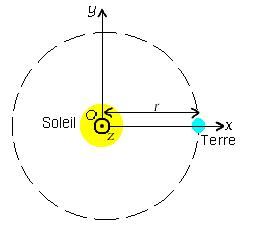
En coordonnées héliocentriques, le plan de référence est l'écliptique et le centre est le Soleil (noté S sur la figure).
La Terre tourne autour du Soleil, en 365 jours 1/4, sur un plan qui est pris comme plan de référence: le plan de l'écliptique ou écliptique (ainsi nommé car les éclipses ont lieu lorsque la Lune est proche de l'écliptique).
|
|
L'orbite de la Terre autour du Soleil n'est pas circulaire mais elliptique.