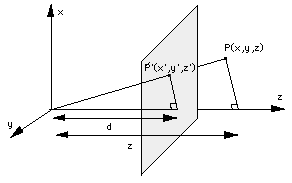
La figure ci-dessous explicite les données du problème. On recherche la matrice qui permet d'obtenir les coordonnées du point P', projeté de P, en fonction des coordonnées du point P.

Le théorème de Thalès fournit immédiatement la solution : des relations
Par suite : [x' y' z' 1 ] = [ x/(z/d) y/(z/d) d 1 ]
|
= |
|
. |
|
| Mper | = |
|