[retour]

Eclairage

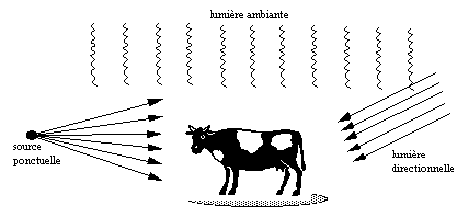
L'éclairement d'un objet par des sources lumineuses est un facteur de "réalisme" très important. Parmi les sources de lumière éventuelles, on distingue la lumière ambiante, caractérisée par une distribution uniforme de l'éclairement, les sources ponctuelles à distance finie de l'objet qui provoquent un clairement radial et les sources à l'infini qui éclairent l'objet avec des rayons lumineux parallèles :

2.1 - Modèle de Phong

Le modèle de Phong peut être résumé en une seule équation exprimant l'intensité lumineuse :

I = I_a + I_d + I_s

où la lumière I reçue par un objet se décompose en lumière ambiante I_a, en lumière diffusée à la surface de l'objet I_d et en lumière réfléchie vers l'observateur I_s ( encore appelée reflet ou lumière spéculaire). Suivant les objets, les deux derniers termes peuvent être très différents : un objet mat aura un I_d fort, un objet réfléchissant aura un I_s fort.

Il reste à donner un moyen de calculer les termes I_d et I_s, le terme I_a n'étant qu'une constante. La lumière diffusée peut être obtenue par la loi de Lambert (fig (a)):

I_d = k_d Σ_iL_i × N

où N est le vecteur unitaire normal à la surface éclairée au point considéré, L_i le vecteur unitaire vers la source i éclairante et k_d un coefficient compris entre 0 et 1 dépendant du matériau et de la longueur d'onde. La lumière spéculaire est usuellement obtenue par la relation(fig (b)) :

I_s = k_s Σ_i(L'_i × N)ⁿ

où L'_iest le vecteur unitaire situé sur la bissectrice de l'angle formé par le rayon vecteur allant du pixel vers la source i et le rayon vecteur allant vers l'observateur, k_s est le coefficient spéculaire et n un entier de 1 à 200 dépendant de la surface.

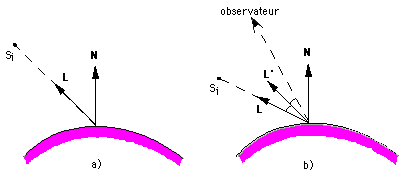
2.2 - Méthodes de Lambert, de Gouraud et de Phong

Le modèle de Phong est simple, mais il nécessite un calcul en chaque point de l'objet, ce qui est très coûteux en temps. Lorsque les objets sont décrits par des facettes polygonales, on emploie usuellement les méthodes de calcul de Lambert, de Gouraud ou de Phong.

La méthode de Lambert suppose que la lumière possède une répartition constante sur une même facette. Ce cas simplificateur correspond à des sources lumineuses à l'infini, à un observateur à l'infini et à une décomposition exacte d'un solide en facettes polygonales. L'intérêt est évident : il n'y a qu'un calcul à faire pour une facette donnée. L'inconvénient est la présence de discontinuité aux limites de facettes.

Pour réduire cet inconvénient, le modèle de Gouraud suppose le calcul de l'intensité lumineuse aux sommets des facettes polygonales, en définissant, pour chaque sommet, un vecteur normal "moyen" :

<N> = 1/Z × Σ_k=1..ZN_k

où cette relation suppose le sommet commun à Z polygones dont les normales sont N_k. A l'intérieur des facettes, l'intensité lumineuse n'est plus constante comme dans le modèle de Lambert mais est calculée par interpolation linéaire à partir de l'intensité lumineuse aux sommets. Le modèle de Phong diffère du modèle de Gouraud par l'interpolation, non de l'intensité, mais du vecteur normal N.

Last modified: Sun Nov 28 20:25:36 CET 2004